La beauté des L-Systèmes
You can also read this article in english.
De quoi s’agit-il ?
Un système de Lindenmayer (communément appelé L-système) est un modèle algorithmique récursif inspiré par la biologie et inventé en 1968 par le biologiste hongrois Aristid Lindenmayer.
Il vise à fournir un moyen de modéliser la croissance de plantes et bactéries.
Le concept fondamental des L-Systèmes est la réécriture, un procédé efficace permettant de générer des objets complexes en remplaçant simplement tout ou partie d’un objet initial.
Nous pouvons envisager cela comme une cellule qui se divise à chaque itération afin de générer un organisme plus abouti.
Si vous êtes curieux, wikipedia en fourni une description plus détaillée.
Très bien, mais en quoi cela peut-il vous intéresser et, plus important encore, que peut-on en faire ?
Il existe une multitude de cas d’usages, certains se sont même amusés à générer de la musique à partir de ceux-là, mais nous allons nous concentrer sur des applications visuelles. Imaginez que vous souhaitez casser la monotonie d’une page web en y ajoutant un motif aléatoire/animé/auto-généré ou bien que vous travailliez sur un jeu et souhaitez y ajouter un décor sans avoir à en pré-générer chaque pixel, ou encore que vous êtes simplement intéressés par le code créatif, les L-Systèmes constituent un excellent point de départ.
La structure d’un L-Système
Premièrement, analysons la structure d’un L-Système (sa grammaire formelle), elle est définie par :
- V un ensemble de symboles remplaçables (variables)
- S un ensemble de symboles non remplaçables (constantes)
- ω une chaîne de caractères constituées de symboles provenant de V, l’état initial du système (axiome)
- P un ensemble de règles de production, définissant comment les symboles provenant de V doivent être interprétés, remplacés par des constantes (S) et/ou des variables (V)
Un L-Système est un tuple, noté {V, S, ω, P} et parfois {V, ω, P} (V et S étant regroupés au sein de V).
Première prise : le flocon de Koch
Nous allons débuter avec une variante du flocon de Koch.
- variables V:
F - constantes S:
+,- - axiome ω:
F - règles P:
F → F+F-F-F+F
Qui va produire :
iteration 0 : F
iteration 1 : F+F-F-F+F
iteration 2 : F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F
La génération est relativement aisée à implémenter en javascript :
const lSystem = ({ axiom: ω, rules: P, iterations: N = 1 }) =>
[...Array(N).keys()]
.reduce(acc => acc.split('').map(s => P[s] ? P[s] : s).join(''), ω)
const result = lSystem({
axiom: 'F',
rules: { F: 'F+F-F-F+F' },
iterations: 2,
})
Donc, après 2 itérations, nous obtenons la chaîne de caractères suivante:
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F
pas très utile en l’état je vous l’accorde, mais considérons maintenant chaque symbole comme une instruction de tracé en utilisant les règles suivantes :
Fdessiner tout droit+tourner à gauche de 90°-tourner à droite de 90°
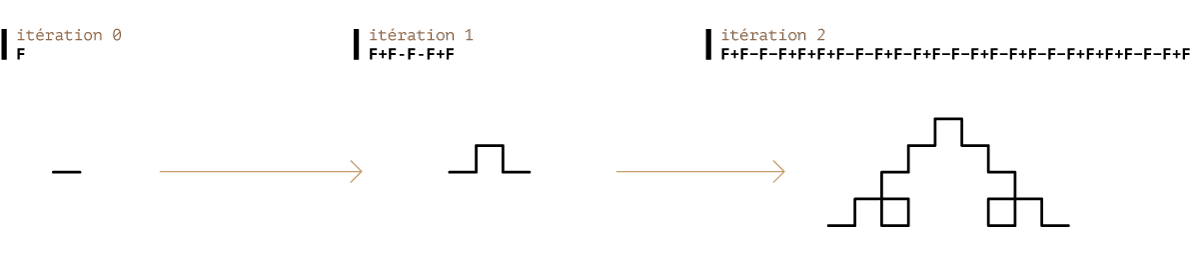
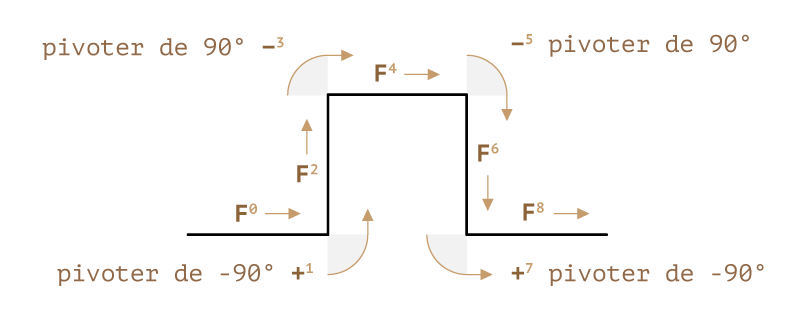
Attardons nous quelque peu sur l’itération 1, F+F-F-F+F, et décomposons en chaque étape :
Vous pouvez utiliser le code suivant afin de générer un tableau de segments à partir du résultat du L-Système (pour des raisons de simplicité, nous utiliserons la librairie victor pour nos vecteurs 2D) :
const { segments } = result.split('').reduce(({ angle, segments }, symbol) => {
if (symbol === '+') return { segments, angle: angle - Math.PI * .5 }
if (symbol === '-') return { segments, angle: angle + Math.PI * .5 }
return { angle, segments: [
...segments,
// nous créons un nouveau sgement, le faisons pivoter en fonction
// de l'angle courant et y ajoutons la précédente position
(new Victor(20, 0)).rotate(angle).add(segments[segments.length - 1]),
]}
}, { angle: 0, segments: [new Victor(0, height)] })
En assumant que vous disposez d’un CanvasRenderingContext2D, vous allez simplement devoir itérer sur ce tableau pour que la magie opère :
“const ctx = canvas.getContext(‘2d’)
ctx.beginPath()
segments.forEach(({ x, y }, i) => ctx[${i === 0 ? 'move' : 'line'}To](x, y))
ctx.stroke()
Pas mal ! En approximativement 30 loc vous avez une illustration générée à partir d’un algorithme, tentez de reproduire celle-ci dans votre éditeur graphique préféré (illustrator, photoshop, krita…), vous constaterez que ce n’est pas si trivial que ça.
Vous pouvez retrouver un exemple de ce code sur codepen.
Il est assez simple d’implémenter le triangle de Sierpinski ou encore la courbe du Dragon en ayant recours à cette technique.

Deuxième prise : une plante fractale
Pour celle-ci nous allons rajouter quelques constantes et variables :
- variables V:
X,FXest juste un espace réservé et ne sera pas interprété durant la phase de rendu - constantes S:
+,-,[,] - axiome ω:
X - règles P:
F → FF,X → F-[[X]+X]+F[+FX]-X
Qui va produire :
iteration 0 : X
iteration 1 : F-[[X]+X]+F[+FX]-X
iteration 2 : FF-[[F-[[X]+X]+F[+FX]-X]+F-[[X]+X]+F[+FX]-X]+FF[+FFF-[[X]+X]+F[+FX]-X]-F-[[X]+X]+F[+FX]-X
Nous pouvons réutiliser le même code que précédemment pour la génération, mais la configuration doit, elle, être modifiée en conséquence :
const result = lSystem({
axiom: 'X',
rules: {
F: 'FF',
X: 'F-[[X]+X]+F[+FX]-X',
},
iterations: 6,
})
Vous aurez probablement noté l’ajout de 2 nouvelles constantes, [ et ] :
[sauvegarder la position et l’angle courant]restaurer la position et l’angle courant à partir de la dernière sauvegarde
Ceci nous donne une pile LIFO permettant de dessiner des lignes non continues, idéale pour représenter les embranchements inhérents à la modélisation d’une plante. Regardons maintenant quel en est le fonctionnement.
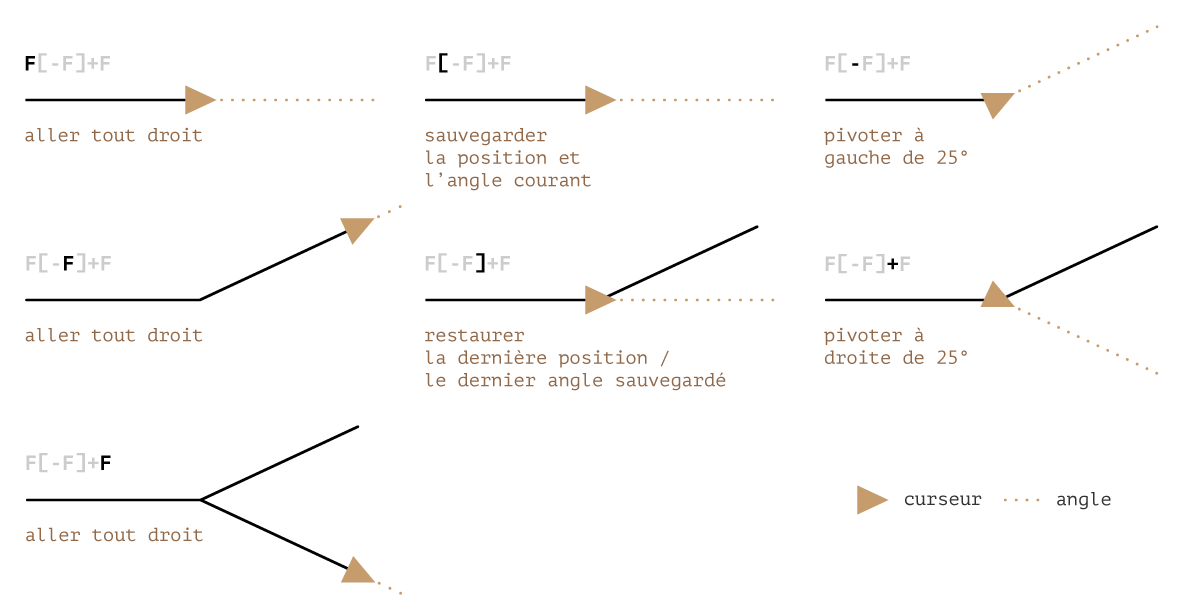
Vous allez devoir modifier le code concernant la génération de segments afin d’y intégrer les nouvelles instructions.
Et comme il ne s’agit plus d’une ligne continue, les segments sont maintenant des objets composés d’un vecteur start et end :
const LENGTH = 6 // longueur de segment
const ANGLE = 25 * Math.PI / 180 // angle utilisé pour les rotations en radians
const ORIGIN = new Victor(0, height * .95) // position initiale
const instructions = {
'-': state => ({ ...state, angle: state.angle - ANGLE }), // tourner à gauche
'+': state => ({ ...state, angle: state.angle + ANGLE }), // tourner à droite
'[': state => ({ // sauvegarder la position courante, l'angle courant
...state,
stack: [ ...state.stack, _.pick(state, ['position', 'angle']) ],
}),
']': ({ stack, ...state }) => { // restaurer la dernière position, le dernier angle sauvegardé
const last = stack.pop()
return { ...state, stack, ...last }
},
'F': state => { // dessiner
const end = new Victor(LENGTH, 0)
end.rotate(state.angle).add(state.position)
return {
...state,
position: end,
segments: [
...state.segments,
{ start: state.position, end },
],
}
},
}
const { segments } = result.split('').reduce(
// si le symbole correspond à une instruction, nous utilisons cette instruction,
// dans le cas contraire, l'état courant est retourné
(state, symbol) => (instructions[symbol] ? instructions[symbol](state) : state),
// état initial
{
angle: -30 * Math.PI / 180, // orientation initiale de l'arbre en radians
position: ORIGIN,
stack: [],
segments: [],
}
)
Nous devons également modifier quelque peu le code concernant le tracé de notre plante :
const ctx = canvas.getContext('2d')
ctx.beginPath()
segments.forEach(({ start, end }) => {
ctx.moveTo(start.x, start.y)
ctx.lineTo(end.x, end.y)
})
ctx.stroke()
Ça y est, nous avons dorénavant tout le code nécessaire à la génération d’un organisme quasiment naturel qui va résulter dans l’illustration utilisée en haut de cette section.
Vous pouvez retrouver un exemple de ce code sur codepen.
Il y a un nombre infini de variations possibles en jouant avec les règles, l’angle ou encore la longueur des segments, si vous lancez une recherche google pour le terme L-Systems, vous trouverez à coup sûr bon nombre de configurations pré-établies.
Conclusion
Merci Aristid ! Je ne pense pas qu’il ait anticipé la popularité à venir lorsqu’il menait ses recherches.
En dehors de fournir un bon moyen pour démarrer avec le code créatif, cet algorithme démontre assez bien que des problèmes complexes peuvent (et devraient) être adressés avec des solutions simples et élégantes. La prochaine fois que vous vous arrachez les cheveux sur un algorithme récursif complexe, ne négligez pas la feinte à base de réécriture !
Si les L-Systèmes vous ont séduit ou que vous êtes intéressés par le code créatif, je ne saurais que trop vous recommander le site internet de Paul Bourke, il ne faut pas se fier au style rudimentaire de celui-ci, c’est une véritable mine d’or !
J’envisage d’écrire une seconde partie à cet article expliquant comment ajouter de l’aléatoire dans un L-Système (utilisant une grammaire stochastique), alors restez connectés !

